Floating-point numbers vs real numbers

Understanding floating-point numbers is essential when working with decimal values. Floating-point numbers may also be used to work with whole numbers that do not fit in a long integer (at the expense of losing precision). In any case, you don’t want to be caught off guard when seeing this:

#Python
>>> r = 72057594037927955
>>> r + 1.0 < r
True

In order to get some intuition about floating-point numbers, it is helpful to consider what problem we are trying to solve by using them.

Let’s first make a detour and take a look at the integer numbers: in any given interval, the number of integers is finite. That property simplifies integers representation. You simply define an interval as large as you are willing to support in your computer architecture and if you ever go beyond the maximum value, you wrap around to the other end of the interval (what is known as modular arithmetic)

//Java
jshell> Integer.MAX_VALUE+1 == Integer.MIN_VALUE
true

Here’s the problem now: given two real numbers, no matters how close they are to each other, it is always possible to find another number in between. That’s another way to say that, in any given interval, there are infinite real numbers.

Standard IEEE 754

To get around this problem, the standard IEEE 754 was devised as a way to take a few numbers as reference so that any other real number would be assigned to one of those pre-selected values. Typically, the way to do that is by using the method: “round to nearest, ties to even”.

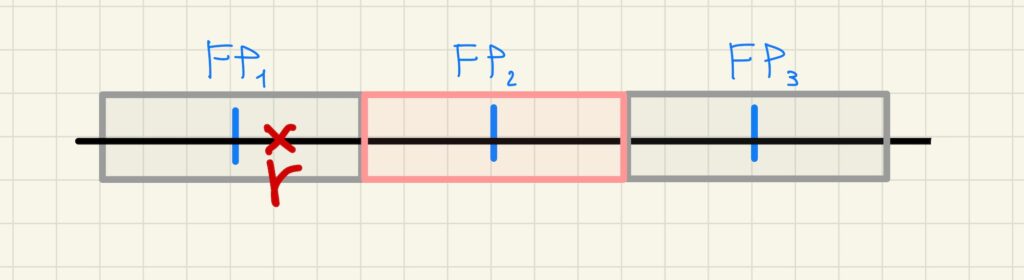
The following figure shows the real number inside the “catchment area” of the floating-point number

#Python
>>> float(72057594037927956)
7.205759403792795e+16

Interestingly enough, Java selects a different value for the floating-point number:

//Java
|  Welcome to JShell -- Version 11.0.11
|  For an introduction type: /help intro

jshell> double d = 72057594037927956d
d ==> 7.2057594037927952E16

The important thing to consider here is that floating-point numbers are defined in binary format, so as long as two decimal numbers have the same binary representation, both are correct. In this case, both and correspond to the same double-precision binary format

0100001101110000000000000000000000000000000000000000000000000001

Actually, there are 15 integers to choose from: … . Not to mention the infinite values resulting of adding a fractional part to each of those integers. So, in a way, floating-point numbers define an equivalence relation on the set of real numbers.

Arguably, the canonical representative would be the exact decimal number, , corresponding to the binary representation. On the other hand, it can be argued that the last digit in the 17-digit is not significant as the 16-digit decimal number is enough to represent the floating-point binary number. And in general this is the preferred approach. The Java behaviour seen above was considered a bug already fixed in newer versions

//Java
|  Welcome to JShell -- Version 21
|  For an introduction type: /help intro

jshell> double d = 72057594037927956d
d ==> 7.205759403792795E16

Precision

From the previous figure it can be derived that:

• the greater the number of floating-point numbers in a given interval, the smaller the distance between them and therefore the fewer real numbers are assigned to the same floating-point number
• all real numbers assigned to the same floating-point number are indistinguishable.

As a result, precision, interpreted as the ability to tell apart numbers arbitrarily close to each other, increases with the number of floating-point numbers.

So when the standard IEEE 754 talks about single and double-precision formats, it is making reference to nothing other than the number of floating-point numbers available in that format.

Let’s get back to the previous example to consider the interval of numbers corresponding to the same floating-point number . In this case, the margin of error will be of up to 7 units, which may not be that bad if we take into consideration that we are dealing with orders of magnitude of ; ultimately it will depend on the use case.

Note: any of the integers in the interval is too large to be represented as a “long” type in Java so they can only be represented as float/double knowing that the actual value of the internal representation may be off by up to 7 units (when using double, and even more for float).

Floating-point vs arbitrary-precision arithmetic

Although precision of floating-point numbers is limited, floating-point arithmetic is fast as it is implemented in hardware by specialised coprocessors called Floating-Point Units (FPU). A FPU contains registers designed specifically to deal with floating-point numbers. For instance, in the x86 architecture, there are 16 128-bit floating-point registers, named xmm0 through xmm15.

On the other hand, if more precision is needed, it is possible to implement arbitrary-precision arithmetic in software. Many programming languages provide libraries to perform arbitrary-precision computations (e.g. BigDecimal in the Java standard library or mpmath in Python).

Here’s a simple example to illustrate the trade-off between precision and speed. The following snippet contains two Python functions to calculate an approximation of pi, one uses floating-point arithmetic and the other arbitrary precision arithmetic:

def double_pi(num_steps):
    step_size = 1.0/num_steps
    sum = 0
    for i in range(num_steps):
        x = (i+0.5)*step_size
        sum += 4.0/(1.0+x**2)
    return step_size*sum

from mpmath import *
def arbitrary_precision_pi(num_steps, precision):    
    mp.dps = precision
    half = mpf("0.5")
    four = mpf(4)
    one = mpf(1)
    step_size = mpf(1)/num_steps
    sum = mpf(0)
    for i in range(num_steps):
        x = (i+half)*step_size
        sum += four/(one+x**2)
    return step_size*sum

For num_steps=1e7, double_pi executes in about 2 seconds. In contrast, arbitrary_precision_pi takes over 2 minutes.

double_pi

% time python pi.py
3.141592653589731
python pi.py  1.70s user 0.02s system 95% cpu 1.802 total

arbitrary_precision_pi

% time python pi.py
3.1415926535897973
python pi.py  121.73s user 0.18s system 99% cpu 2:02.32 total

References

Floating-point converter